Distribuição de Poisson na Construção Civil: Exemplo Da Utilização De Distribuição De Poisson Na Construção Civil
Exemplo Da Utilização De Distribuição De Poisson Na Construção Civil – A construção civil, com suas inúmeras variáveis e eventos aleatórios, apresenta desafios significativos na gestão de projetos. A imprevisibilidade inerente a este setor demanda ferramentas estatísticas robustas para prever riscos, otimizar recursos e tomar decisões informadas. Neste artigo, exploraremos a aplicação da distribuição de Poisson, uma ferramenta poderosa para modelar eventos discretos e aleatórios, no contexto da construção civil.
Introdução à Distribuição de Poisson
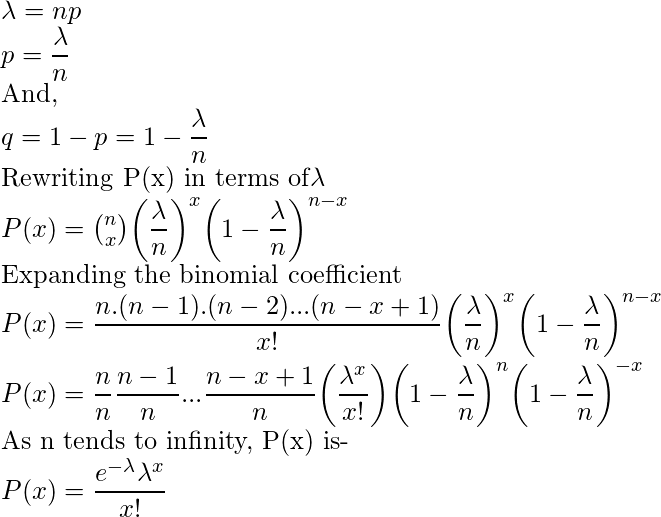
A distribuição de Poisson é uma distribuição de probabilidade discreta que descreve a probabilidade de um determinado número de eventos ocorrerem em um intervalo de tempo ou espaço fixo, dado que a taxa média de ocorrência desses eventos é conhecida e constante. Sua principal propriedade é a independência dos eventos: a ocorrência de um evento não afeta a probabilidade de ocorrência de outro evento.
A fórmula para calcular a probabilidade de x eventos ocorrerem é dada por: P(X=x) = (e^-λ
– λ^x) / x!, onde λ representa a taxa média de ocorrência e e é a constante de Euler (aproximadamente 2,71828).
Eventos aleatórios independentes são eventos cuja ocorrência não influencia a probabilidade de ocorrência de outros eventos. Na distribuição de Poisson, assume-se que os eventos são independentes. Por exemplo, a chegada de caminhões em um canteiro de obras é considerada independente se a chegada de um caminhão não afeta a probabilidade de chegada de outro. A distribuição de Poisson encontra aplicações em diversas áreas além da construção civil, como em telecomunicações (número de chamadas em um call center), medicina (número de pacientes em uma emergência), e finanças (número de transações em um determinado período).
Cenários na Construção Civil Adequados à Distribuição de Poisson
Vários cenários na construção civil se beneficiam da modelagem com a distribuição de Poisson. Três exemplos relevantes são:
- Defeitos em materiais: A quantidade de tijolos defeituosos em um lote de produção.
- Acidentes de trabalho: O número de acidentes em um canteiro de obras ao longo de um determinado período.
- Atrasos na entrega de materiais: A quantidade de atrasos na entrega de materiais de construção em um projeto.
A aplicação da distribuição de Poisson em projetos de grande porte difere da aplicação em projetos menores principalmente pela escala. Em grandes projetos, a taxa média (λ) tende a ser maior, resultando em uma maior variabilidade nos resultados. Em projetos menores, a taxa média é tipicamente menor, levando a uma menor variabilidade. Entretanto, em ambos os casos, a premissa de independência dos eventos deve ser cuidadosamente avaliada.
Em situações complexas, com múltiplas variáveis interdependentes, a distribuição de Poisson pode apresentar limitações, necessitando de modelos mais sofisticados.
| Evento | Taxa Média (λ) | Intervalo de Tempo | Probabilidade de Ocorrência |
|---|---|---|---|
| Defeitos em tijolos | 0.05 defeitos/100 tijolos | Lote de 1000 tijolos | Calculada pela fórmula de Poisson |
| Acidentes de trabalho | 1 acidente/mês | 1 ano | Calculada pela fórmula de Poisson |
| Atrasos em entregas | 2 atrasos/semana | 1 mês | Calculada pela fórmula de Poisson |
Exemplos Práticos de Aplicação
Vamos detalhar a aplicação da distribuição de Poisson em três cenários específicos:
Previsão de Defeitos em Linha de Produção de Tijolo
Suponha uma linha de produção de tijolos com uma taxa média de defeitos de 0,1 tijolos defeituosos por cada 100 tijolos produzidos. Desejamos calcular a probabilidade de encontrar exatamente 2 tijolos defeituosos em um lote de 500 tijolos. Primeiro, calculamos a taxa média para o lote de 500 tijolos: λ = (0,1/100)
– 500 = 0,
5. Aplicando a fórmula de Poisson, obtemos a probabilidade:
| Número de defeitos (x) | Probabilidade P(X=x) |
|---|---|
| 0 | 0.6065 |
| 1 | 0.3033 |
| 2 | 0.0758 |
| 3 | 0.0126 |
Modelagem do Número de Acidentes de Trabalho
Em um canteiro de obras, a taxa média de acidentes de trabalho é de 2 acidentes por ano. Podemos utilizar a distribuição de Poisson para prever a probabilidade de ocorrerem 0, 1, 2, ou mais acidentes em um determinado ano. Neste caso, λ = 2. A probabilidade de cada cenário pode ser calculada utilizando a fórmula da distribuição de Poisson.
Previsão de Atrasos em Entregas de Materiais
Considere um projeto de construção onde a taxa média de atrasos na entrega de materiais é de 1 atraso por semana. A distribuição de Poisson pode ser utilizada para modelar a probabilidade de ocorrerem diferentes números de atrasos em um período de tempo específico, como um mês (4 semanas).
Métodos de Cálculo e Análise, Exemplo Da Utilização De Distribuição De Poisson Na Construção Civil

A probabilidade de x eventos ocorrerem, seguindo a distribuição de Poisson, é calculada utilizando a fórmula: P(X=x) = (e^-λ
– λ^x) / x!, onde λ é a taxa média de ocorrência e x é o número de eventos. Um exemplo numérico: Se λ = 3 e queremos calcular a probabilidade de ocorrerem exatamente 2 eventos, temos: P(X=2) = (e^-3
– 3^2) / 2! ≈ 0,224.
A interpretação do resultado depende do contexto. Em construção civil, uma alta probabilidade de atrasos, por exemplo, indica a necessidade de medidas preventivas. Softwares estatísticos como R, SPSS e Excel possuem funções para calcular probabilidades de Poisson, facilitando a análise e a tomada de decisões.
Considerações e Limitações
A distribuição de Poisson auxilia na tomada de decisões, permitindo a quantificação de riscos e a alocação eficiente de recursos. No entanto, é crucial reconhecer suas limitações. A premissa de independência dos eventos é fundamental; se os eventos são dependentes, a distribuição de Poisson não é adequada. Além disso, a taxa média (λ) deve ser constante no intervalo considerado.
Em cenários complexos, com múltiplas variáveis interdependentes, a distribuição de Poisson pode fornecer apenas uma aproximação, e modelos mais sofisticados podem ser necessários. A distribuição binomial, por exemplo, pode ser mais apropriada quando o número total de tentativas é fixo e a probabilidade de sucesso é constante.
Quais softwares podem ser utilizados para calcular a distribuição de Poisson?
Softwares estatísticos como R, SPSS e Excel (com suas extensões) permitem cálculos de probabilidade utilizando a distribuição de Poisson.
A distribuição de Poisson é adequada para modelar eventos dependentes?
Não. A distribuição de Poisson pressupõe eventos independentes. Em casos de dependência, outras distribuições probabilísticas podem ser mais apropriadas.
Como lidar com dados que não se ajustam perfeitamente à distribuição de Poisson?
Técnicas de transformação de dados ou a utilização de outras distribuições probabilísticas podem ser necessárias quando o ajuste não é ideal.

